樹在資料結構中是一種由數個節點 (Node) 所組成的一種有上下關係的結構。
樹的特色是:
- 除了根節點 (root) 以外,每個節點都會有一個父節點
- 每個節點都可以有零個或多個節點
- 從根節點開始我們可以順著走到每一個節點
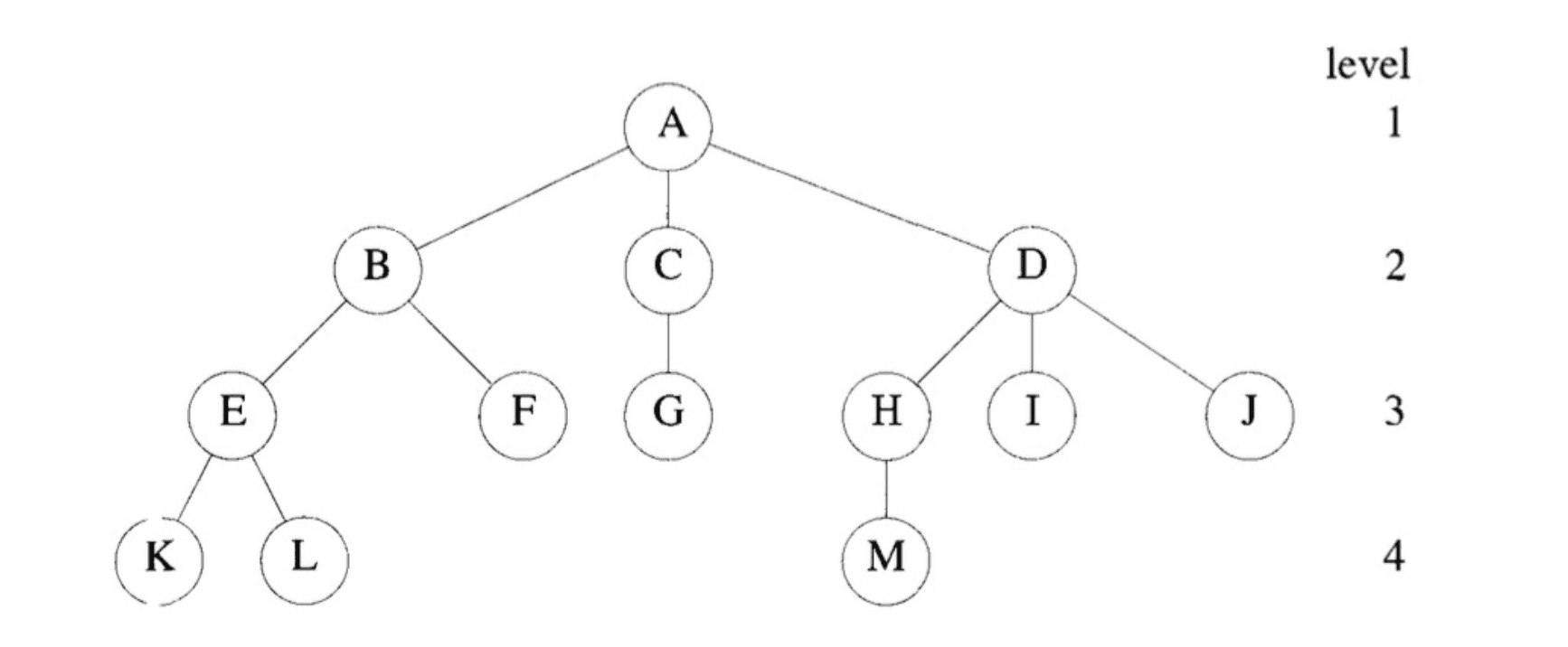
那現在就上我們配著上面這張圖來介紹一些在樹裡面會常見到的詞吧!
- 節點 (Node): 在樹裡面的每個元素我們都稱之為節點,如上圖中的 A - M 都是一個一個的節點
- 父節點 (Parent Node):可以看圖中的 A 點,因為從他伸出了 B、C、D 三點,所以我們稱 A 是 B、C、D 三點的父節點
- 子節點 (Child Node): 相對於 A 是 B、C、D 的父節點;B、C、D 三點就是 A 的子節點
- 兄弟節點 (Sibling Node):圖中的 B、C、D 三點互相是對方的兄弟節點,也就是在樹中同一層的節點
- 根節點 (root):這也就是圖中的 A 點,是整棵樹的起點,也是唯一一個沒有父節點的節點
- 葉節點 (leaf):圖中的 K、L、M 三點,是整棵樹的最下層,也就是只有父節點沒有子節點的節點
- 祖先節點 (Ancestor Node):一個節點往上到根節點的路上每個節點都稱為他的祖先節點
- 子孫節點 (Descendant Node):一個節點往下到葉節點的路上每個節點都是他的子雖節點
- 度 (Degree):一個節點的子節點數量。例如圖中的 A 節點因為有 B、C、D 三個子節點所以他就是 3 度
- 深度 (Depth):根節點到某一個子節點的層數就是那個子節點的深度,例如 I 節點到根節點 A 中間有 3 層,所以他的深度就是 3
- 高度 (Height):整棵樹有幾層,也可以說是整個樹深度的最大值,例如圖中的樹高度就是 4
- 森林 (Forest):一個由很多顆樹組成的集合就稱為森林
二元樹 Binary Tree
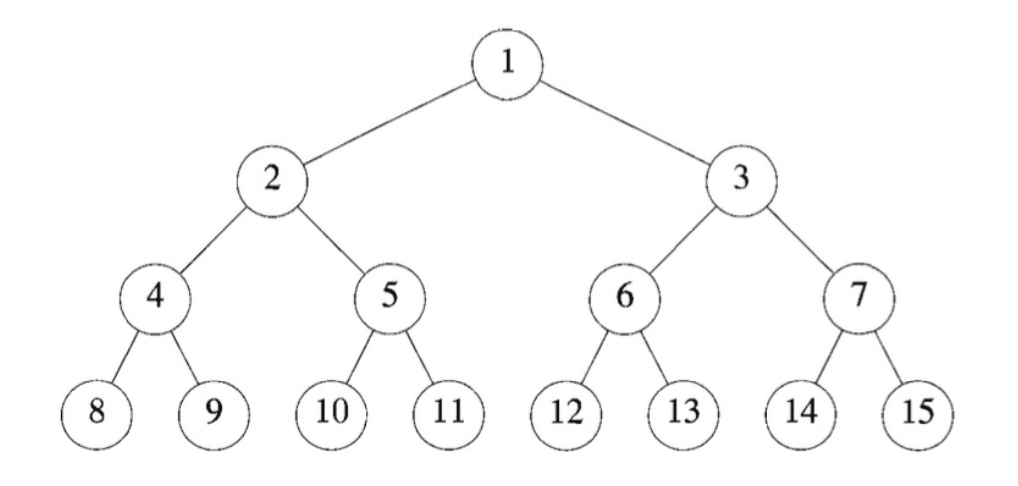
二元樹是一種很常見的樹,他的規則就是每個節點都最多只能有兩個子節點(可以 0, 1, 2 個),若一個節點有兩個子節點,我們就把他的子節點取名為左子節點 (Left Child) 和右子節點 (Right Child)
二元樹的另外一個特性就是我們可以順利的從上到下從左到右的幫每一個節點編碼,這個特性可以方便我們快速找到每個節點的父節點,並且可以把樹存在陣列當中
滿二元樹 (Full Binary Tree)
如果一個二元樹的非葉節點都有 2 個子節點,且所有葉子都在同一層(如上圖),這個深度為 k 的樹就會有 2^k - 1 個節點,且我們稱它為 滿二元樹(Full Binary Tree)
完全二元樹 (Complete Binary Tree)
如果一個二元樹除了最後一層之外,所有層都必須填滿節點,最後一層的節點必須從左到右填入,那我們就稱它為 完全二元樹
完全二元樹在應用中具有很多優點,例如:
- 可以使用陣列來存儲,這樣可以減少存儲空間(因為不用存 key 值)。
- 可以用來實現堆(Heap)等高效的數據結構,進而用於排序、優先級佇列等操作。
- 可以用於搜索二元樹(Binary Search Tree)的平衡化,將搜索二元樹轉換為平衡二元樹,以提高搜索、插入和刪除的效率。
二元樹是一個在資工領域中超級常用的資料結構,今天介紹了一些基本的名詞解釋,明天就會進入開始介紹這些二元樹的實際應用。