上次介紹了樹是什麼,還有一些常見種類的樹,但那都只討論到一棵樹的範圍,今天就來探討一下如果有多棵樹的話,我們要怎麼把它結合起來,以及我們要如何找到一個 Node 存在哪棵樹裡面
Sets
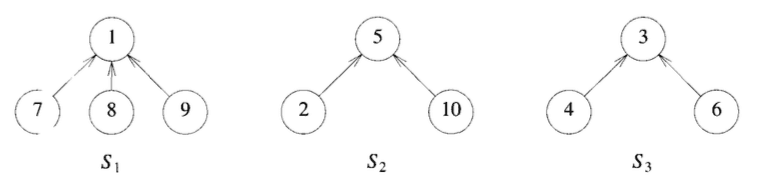
Sets 其實指的就是 forest 的應用,也就是對大於一棵樹進行操作。在這邊我們討論的是 disjoint 的 forest,也就是説在不同的 sets 裡面不會有相同的 Node。
而在這些 sets 裡面我們就要討論如何 合併(Union) 兩個 sets 以及如何 尋找(Find) node 在哪一個 set 裡面不會有相同的
合併和尋找 (Union and Find)
1. 合併 (Union)
要合併兩個 tree,我們最簡單的方法就是把整個樹整顆從 root 到所有的 subtree 都變成另外一個樹的一個 subtree
2. 尋找 (Find)
在說這個之前我們需要先提到 set 的資料表達法。
By Pointer

這個表示方式比較直觀,就是把這些 trees 存在一個 table 裡面,用一個 set name 來代表每一個 set,然後再用一個 pointer 指向那一個 set 的 root。這時候我們就用 name[root] 來表示這一個 tree
在 By Pointer 的表達方式中,Find 其實很簡單,只要往上找到那個 node 的 root,之後在到 table 裡面找到他的 pointer 就可以知道他在哪個 set 裡面了。
By Array

這種作法是一個更節省空間的做法,我們把所有 node 放在一個 index 為 1 到 node 數量的陣列裡面,在 array 裡面的值就會放那個 node 的 parent,然後如果沒有 parent 的話就代表他是 root,所以就用 -1 來代表他的值。
在 By Array 的表達方式,Find 就是從那個 node 的值開始一步一步往上找,如果找到值為 -1 的就代表找到 root 了,因為這個表達法比較省空間,所以後續的範例都會用這種表示方式
// 把 Union 跟 Find 寫成 Psuedo Code
Alogrithm SimpleUnion(i, j) {
p[i] = j //把 i 併入 j
}
Alogrithm SimpleFind(i,j) {
while(p[i] >= 0) {
i = p[i] //還沒找到 root 就往他的 parent 找
}
return i
}
雖然說 SimpleFind 跟 SimpleUnion 可以很容易地解決問題,但這兩個因為要一個一個動作,所以他們的效能不太好。
假設今天有 8 個只有一個 node 的 tree 要進行 union 就需要 8 次合併,所以他的時間複雜度就會是 O(n)
那如果是要找 8 個 node 的話,每一個元素都需要從下往上,所以是 O(n),那找 n 個元素就會是 O(n^2)
Weighting Rule
這個 weight rule 就是效能不好的解法,他的核心概念就是當我們要合併 2 個 tree 的話,會把 children 數量比較少的 tree 合併到比較多的那個樹。
這樣做的話,如果是 n 顆數進行合併,合併之後的樹高度就不會超過 log2N + 1,舉例來說,如果有 8 個只有一個 node 的樹合併,在使用 SimpleUnion 的情況下會是 8 層,但是在 WeightedUnion 的情況下就會是 log22 + 1 的 2 層。
在這樣有限高度的情況下,尋找 n 個元素的時間複雜度就會變為 O(n)
Algorithm WeightedUnion(i, j) {
p[i] = count[i] * -1, p[j] = count[j] * -1
temp = p[i] + p[j];
if(p[i] > p[j]) {
p[i] = j;
p[j] = temp;
} else {
p[j] = i;
p[i] = temp
}
}
Quiz
在這邊可以想一下為什麼 p[i] 和 p[j] 要是負數?
Answer
在 by array 的表示方法下,正數的值表示的是那個 node 的 parent,所以使用負數來區分出 root 跟其他 node
Collapsing Rule
雖然 Weighting Rule 已經可以提升 find 的效能,但還有一個方式可以更加提升效率,就是 Collapsing Rule
他的概念就是在 Find 的時候如果要找的 node 他的 parent 不是 root 的話就把他 parent 那個 subtree 直接移到整棵樹的 root 上面
這樣雖然在每一次搜尋的時候會多一個步驟稍微拖慢一下每次搜尋的效率,但是這樣可以壓縮樹,讓下一次的搜尋更加快速!
Alogrithm CollapsingFind(i) {
//找到 i 的 root,並且利用 collapsing rule 壓縮樹
r = i;
while(p[r] > 0) {
r = p[r]; //找到 i 的 root
}
while(i != r) { //把 subtree 移動到 root 上
s = p[i];
p[i] = r;
i = s;
}
return r
}
介紹完 sets 之後,在資料結構的部分就只剩下 graph 了!那就期待一下吧!